BIO
An Academic’s Story
I received my Ph.D. degree from Auburn University in 2010, where I wrote my thesis on fixed points of orientation reversing homeomorphisms of the plane, under guidance of K. Kuperberg. My Habilitation degree is from 2019, and it was on the topic of inverse limit techniques in topology and theory of dynamical systems. M. Misiurewicz, T. Downarowicz and M. Lemańczyk were the referees.
More complete CV can be found here.
NCN FUNDED RESEARCH
(SONATA BIS)
Topological and Dynamical Properties in Parameterized Families of Non-Hyperbolic Attractors: the inverse limit approach (2020-2025).
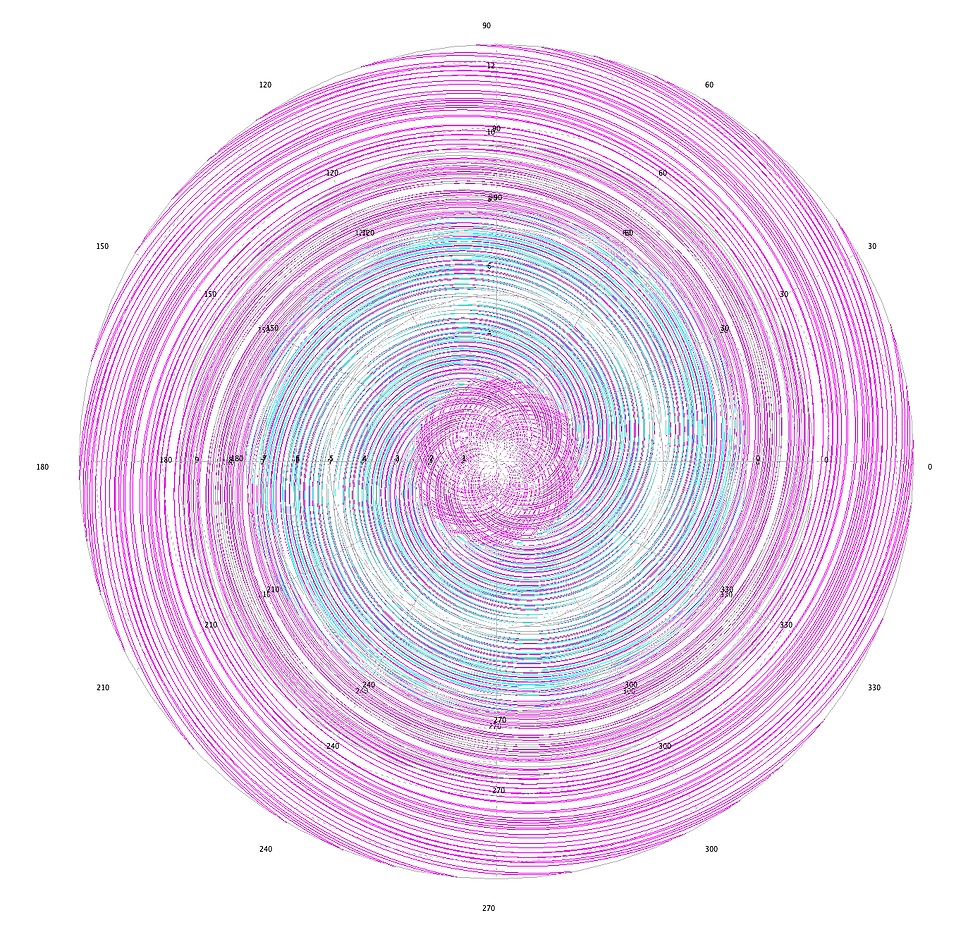
019/34/E/ST1/00237; Principal Investigator: dr hab. Jan Paweł Boroński
019/34/E/ST1/00237; Principal Investigator: dr hab. Jan Paweł Boroński

019/34/E/ST1/00237; Principal Investigator: dr hab. Jan Paweł Boroński

019/34/E/ST1/00237; Principal Investigator: dr hab. Jan Paweł Boroński
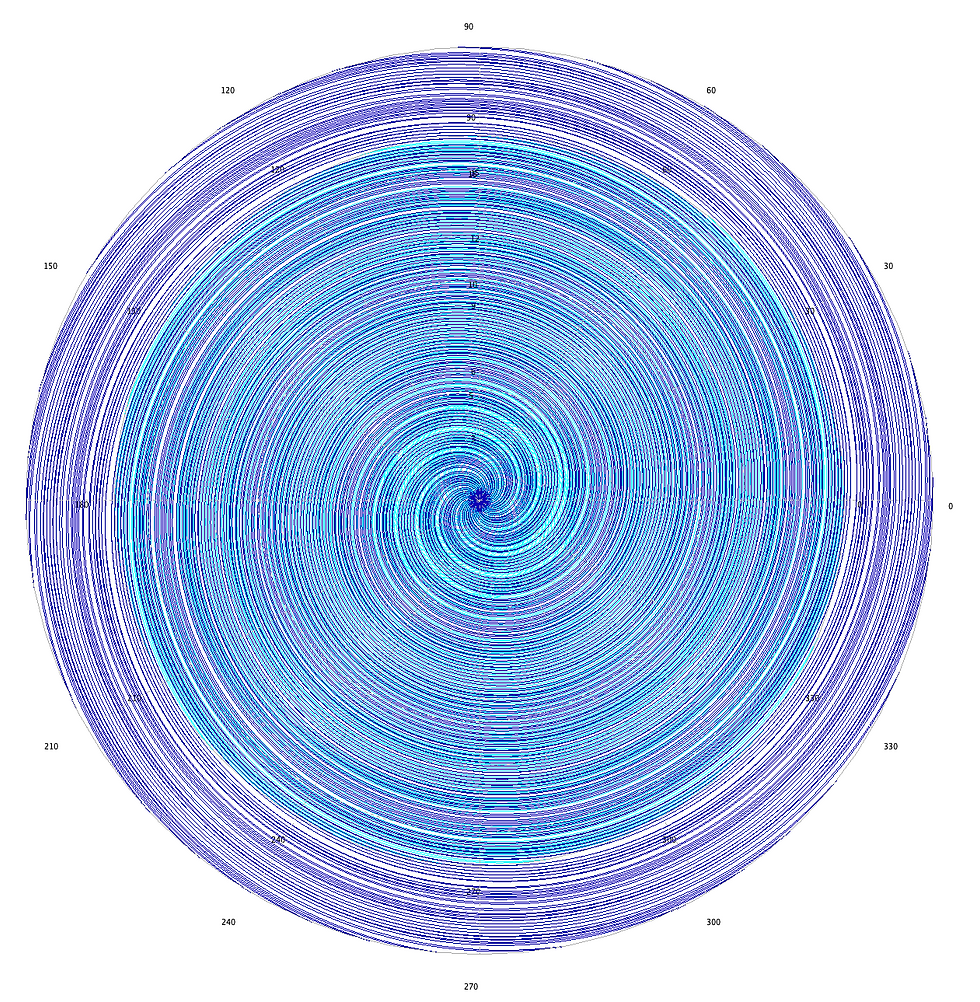
NAWA (POLAND) - OEAD (AUSTRIA) GRANT
Aperiodic Zero-Dimensional Systems (2022&2023)
AGH University of Science and Technology (P.I. J. Boroński) - University of Vienna (P.I. H. Bruin)

SELECTED WORK
My Research

DENSELY BRANCHING TREES AS MODELS FOR HENON-LIKE AND LOZI-LIKE ATTRACTORS
June 23, 2023
In a joint work with S. Stimac (Zagreb) we show that Henon-like and Lozi-like maps on their strange attractors are conjugate to natural extensions (a.k.a. shift homeomorphisms on inverse limits) of maps on metric trees with dense set of branch points. In consequence, these trees very well approximate the topology of the attractors, and the maps on them give good models of the dynamics. To the best of our knowledge, these are the first examples of canonical two-parameter families of attractors in the plane for which one is guaranteed such a 1-dimensional locally connected model tying together topology and dynamics of these attractors. Our result can be seen as a generalization to the non-uniformly hyperbolic world of a classical result of Williams from 1967. We also show that no simpler 1-dimensional models exist.
Boronski J., Stimac S; Densely branching trees as models for Henon-like and Lozi-like attractors, Advances in Mathematics, 429 (2023) 109191

ON CONJUGACY OF NATURAL EXTENSIONS OF 1-DIMENSIONAL MAPS
September 20, 2022
In a joint work with P. Minc and S. Štimac we prove that for any nondegenerate dendrite D there exist topologically mixing maps F:D→D and f:[0,1]→[0,1], such that the natural extensions (aka shift homeomorphisms) σF and σf are conjugate, and consequently the corresponding inverse limits are homeomorphic. Moreover, the map f does not depend on the dendrite D, and can be selected so that the inverse limit of (D,F) is homeomorphic to the pseudo-arc. The result extends to any finite number of dendrites. Our work is motivated by, but independent of, the recent result of the first and third author on conjugation of Lozi and Hénon maps to natural extensions of dendrite maps.
Boronski J., Minc, P., Stimac S; On conjugacy of natural extensions of 1-dimensional maps, Ergodic Theory and Dynamical Systems, doi:10.1017/etds.2022.62
MINIMAL MANIFOLDS
May, 2020
Fathi and Herman showed that every compact connected manifold which admits a smooth, locally free effective action of the circle group has a smooth diffeomorphism, isotopic to the identity,which is minimal, and so all odd dimensional spheres admit a minimal diffeomorphism. Every manifold that admits a minimal flow admits also a minimal homeomorphism. The converse does not hold even in dimension 2, as manifested on the Klein bottle. Less have been known about the existence of minimal noninvertible maps. The circle does not admit such maps, despite admitting minimal rotations. Both the 2-torus and Klein bottle admit minimal noninvertible maps, but in dimension at least 3 it has not been known which manifolds admit minimal noninvertible maps. By application of a result of Béguin, Crovisier and Le Roux, here we show that any compact manifold of dimension at least 2 admits a minimal noninvertible map if it admits a minimal homeomorphism. Consequently, our result combined with a result of Fathi and Herman gives, what one might call, a counterexample to a ”noninvertible Gottschalk Conjecture".
Boronski J.P., Kozlowski G. On minimal manifolds, Proceedings of the American Mathematical Society, 149 (2021) 2669-2672
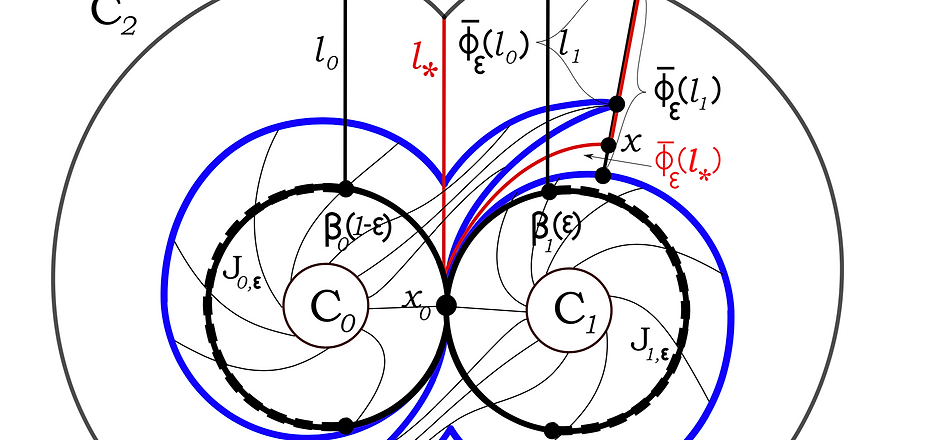
PRIME ENDS DYNAMICS IN PARAMETRISED FAMILIES OF ROTATIONAL ATTRACTORS
January 31, 2020
In a joint work with J. Cinc (Ostrava) and X-C. Liu (Sao Paulo) we study bifurcations, as well as continuity and monotonicity of the accessible rotation number in parametric families of planar attractors. This includes natural extensions of a particular subfamily of Arnold' Standard Family on the circle. The latter has applications in modelling driven mechanical rotors, phase-locked loop in electronics, acoustically coupled musical instruments, and cardiac rhythms.
Boronski J.P.; Cinc J., X-C. Liu, Prime Ends Dynamics in Parametrised Families of Rotational Attractors, Journal of the London Mathematical Society, doi:10.1112/jlms.12328

RIGID MINIMAL SPACES
March 10, 2020
We consider rigid minimal spaces, motivated by recent results of Downarowicz, Snoha, and Tywoniuk on spaces with cyclic group of homeomorphisms generated by a minimal homeomorphism, and results of Boronski, Clark and Oprocha on spaces in which the square of every homeomorphism is a power of the same minimal homeomorphism. We show that the two classes do not coincide, which gives rise to a new class of spaces that admit minimal homeomorphisms, but no minimal maps. We modify the latter class of examples to show for the first time existence of minimal spaces with degenerate homeomorphism groups. Finally, we give a method of constructing decomposable compact and connected spaces with cyclic group of homeomorphisms, generated by a minimal homeomorphism, answering a question in Downarowicz et al.
Boronski J.P.; Cinc J., Forys-Krawiec, M. On rigid minimal spaces, Journal of Dynamics and Differential Equations, DOI 10.1007/s10884-020-09845-4

ALL CANTOR MINIMAL SYSTEMS ARE SLOW
2019
In a joint work with P. Oprocha and J. Kupka (Ostrava) we investigate dynamical systems on the 0-dimensional fractal called Cantor set. We show that all systems that are minimal (i.e. all points travel arbitrarily close to any given location under iterations of the system) can be realized as systems with zero derivative at every point. This includes minimal systems with infinite entropy.
Boronski J.P.; Kupka J.; Oprocha P., All minimal Cantor systems are slow, Bulletin of the London Mathematical Society 51 (2019)
Boronski J.P.; Kupka J.; Oprocha P., Edrei's Conjecture revisited, Annales Henri Poincaré 19 (2018)

MINIMAL SPACES WITHOUT MINIMAL SQUARES
2018
In a joint work with A. Clark (Queen Mary University of London) and P. Oprocha (AGH) we show that the property of admiting minimal homeomorphisms is not preserved under taking Cartesian powers.
Boronski J.P.; Clark A.;Oprocha P., A compact minimal space Y such that its square YxY is not minimal, Advances in Mathematics, 335

MIXING ON SIERPINSKI CARPET
2018
We construct dynamical systems on the fractal called Sierpinski Carpet, that have a strong form of chaosity called topological mixing.
Boronski J.P.; Oprocha P., On dynamics of the Sierpinski Carpet, Comptes Rendus Mathématique Académie des Sciences Paris, 356

LI-YORKE CHAOS
2017
In a joint work with J. Kupka (Ostrava) and P. Oprocha we discover a mixing system on the Cantor set, that is Li-Yorke chaotic at every point.
Boronski J.P.; Kupka J.; Oprocha P., A mixing completely scrambled system exists, Ergodic Theory and Dynamical Systems 39 (2019)

FIXED POINTS OF PLANAR HOMEOMORPHISMS
2017
In 1951 Cartwright and Lttlewood proved a fixed point theorem for planar homeomorphisms with an acyclic invariant continuum, motivated by their study of the Van der Pol differential equation. In my paper, I generalize their result to non-invariant continua.
Boronski J.P., On a generalization of the Cartwright-Littlewood fixed point theorem for planar homeomorphisms, Ergodic Theory and Dynamical Systems 37

CHAOS VS. INDECOMPOSABILITY
2015
In a joint work with P. Oprocha we show that even though natural extensions of positive entropy maps embed in the plane with attractors that must contain indecomposable continua, the same principle in not true for the slightly weaker form of chaos, that is Li-Yorke chaos.
Boronski J.P.; Oprocha P.,On indecomposability in chaotic attractors, Proceedings of the American Mathematical Society143

A NEW COUNTEREXAMPLE TO WOOD'S CONJECTURE
2018
In a joint work with M. Smith (Auburn University) we discover a new counterexample to the Conjecture of Wood in isometric theory of Banach spaces.
Boronski J.P.; Smith M., On the Conjecture of Wood and Projective Homogeneity, Journal of Mathematical Analysis and Applications 461

BIRKHOFF-LIKE ATTRACTORS
2015
In a joint work with P. Oprocha we discover Birkhoff-like attractors that are pseudo-circles. This shows that rotational attractors can have a pathological structure of a bad fractal.
Boronski J.P.; Oprocha P., Rotational chaos and strange attractors on the 2-torus, Mathematische Zeitschrift 279
Get in touch to learn more.

RECENT COURSES
GRADUATE COURSE
Fall 2023
Smooth Dynamical Systems lecture and lab for mathematics masters students at Jagiellonian University
UNDERGRADUATE COURSE
Fall 2023
Ordinary Differential Equations lecture for math undergrads at Jagiellonian University
UNGRADUATE COURSE
Spring 2023
Ergodic Theory lab at Jagiellonian University
GRADUATE COURSE
Fall 2021
Mathematics Research Design and Methodology class for Ph.D. students of Faculty of Applied Mathematics at AGH
UNDERGRADUATE COURSE
Falls 2019-2021
Mathematical Analysis class for the students enrolled in Computer Science in English Program, Faculty of Electrical Engineering, Automatics, Computer Science and Biomedical Engineering, AGH University of science and Technology
UNDERGRADUATE COURSE
Falls 2019-2021
Higher Algebra class for the students enrolled in Computer Science in English Program, Faculty of Electrical Engineering, Automatics, Computer Science and Biomedical Engineering, AGH University of science and Technology
UNDERGRADUATE COURSE
Springs 2020,2022
Differential Equations class for the students enrolled in Computer Science in English Program, Faculty of Electrical Engineering, Automatics, Computer Science and Biomedical Engineering, AGH University of science and Technology
MINICOURSE
June 2018
Minicourse on Fixed Point Theory and Minimal Systems at Workshop on Continuum Theory and Hyperspaces, Universidad Autónoma de Querétaro, Mexico
MINICOURSE
May 2017
Minicourse on Fixed Point Theory and Minimal Systems, Vienna Doctoral School of Mathematics, University of Vienna
UNDERGRADUATE COURSE
January - May, 2013
Honors Calculus 2, Auburn University

